MCMC (Markov Chain Monte Carlo) 샘플링
- IT/머신러닝
- 2020. 4. 12. 20:12
MCMC는 진짜... 해도해도 이해가 안가고 할수록 더 이해가 안가는 모델인 것 같다.... 원래 논문 실험을 할 때 샘플링을 할 일이 있어서 (결국 안쓰게 됐지만) 그때 MCMC를 정리해놨던게 있는데 여기에 올린다.
일단, 위키백과에 따르면 MCMC(Markov Chain Monte Carlo, 마코프체인 몬테카를로)란 '마르코프 연쇄의 구성에 기반한 확률 분포로부터 원하는 분포의 정적 분포를 갖는 표본을 추출'하는 알고리즘의 한 부류이다. 쉽게 말하면 어떤 목표 확률분포(Target Probability Distribution)로부터 랜덤 샘플을 얻는 방법이라고 할 수 있다.
마코프 체인(Marcov Chain)
마코프 체인에서의 체인을 쓴 것은 상태값이 독립이 아니라 이전의 상태에 영향을 받기 때문이다. 장마가 오고있는 상황을 가정한다면, 어제 비가 왔을 때 오늘도 비가 올 확률이 화창할 확률보다 더 높을 것이다. 그리고 이것은 이전 상태에 영향을 받는 것이기 때문에 아래와 같이 조건부 확률로 표현할 수 있다.

여기서 k=시간, Xk=상태값(k=시간) 이다. 그리고 위 마코프 체인 설명에서 각 상태는 바로 이전의 상태에'만' 영향을 받는다고 가정했기 때문에 아래와 같이 수식을 고칠 수 있다.

몬테카를로(Monte Carlo)
계산하려는 값이 복잡한 경우에 난수를 이용하여 함수의 값을 확률적으로 계산하는 알고리즘이다. 예를들어, 반지름이 1인 원의 넓이를 원의 넓이를 구하는 공식을 사용하는 것 말고 아래와 같이 구할 수 있다.
원점을 중심으로 한 변의 길이가 2인 정사각형 생성
정사각형 내부에 무작위 난수를 생성
원점으로부터 거리가 1 이하인 점의 비율을 계산
계산된 비율에 사각형의 넓이를 곱하여 원의 넓이를 추정
MCMC (Markov Chain Monte Carlo)
MCMC 알고리즘은 우리가 샘플을 얻으려고 하는 목표분포를 Stationary Distribution으로 가지는 마코프 체인을 만든다. 이 체인의 시뮬레이션을 가동하고 초기값에 영향을 받는 burn-in period를 지나고 나면 목표분포를 따르는 샘플이 생성된다.
문제는 어떻게 그런 마코프 체인을 만들 수 있냐는 건데, 잘 알려진 방법으로 Metropolis와 이를 일반화한 Metropolis-Hastings, 그리고 깁스 샘플링(Gibbs Sampling)이 있다. 날씨 마코프 체인에서 전이확률을 이용해 다음날의 날씨를 예측했듯이 이들 알고리즘들은 현재 상태에 기반해서 다음 샘플을 만드는 나름의 방법을 제시한다.
샘플링 (Sampling)
복잡한 확률 모델들은 정확한 확률값들을 추론(inference)하기가 불가능하다. 실제적으로 확률 모델을 사용하는데 있어서 확률값의 정확한 추론이 불가능하기 때문에 근사 기법들에 의지 할 수 밖에 없는데, 이런 근사 기법 들 중 하나가 sampling 기법이다. 실제 모델을 통해 어떠한 값을 예측하는데에는 기대값(expectation)을 구하는 것이 중요한 포인트인데 샘플링을 통해 어떻게 기대값을 구할 수 있는지 보자.
우선 어떤 분포 p(x)가 있다고 가정하고 x에 관한 함수 f(x)가 있다고 가정했을때. 우리가 관심이 있는 부분은 어떻게 하면 f(x)의 기대값인 E[f]를 구할 수 있는가 하는 문제이다. 이는 간단히 아래와 같이 나타낼 수 있다. 만약 x가 이산 확률 변수였다면 이 식을 적분 식이 아니라 합의 공식으로 표현되었을 것이다.

어쨌든! 샘플링을 하려는 목적은, 기대값을 구하는 것이 쉽지가 않기 때문에 샘플링을 통한 기대값 근사를 하려고 하는 것이다. 샘플링 기법은 여러가지이지만 Rejection Sampling, Metropolice Hastings를 살펴보자.
Rejection Sampling
우리가 샘플링하고 싶은 목표 분포(target distribution)는 ~p(z)이다(~은 근사값이라는 것을 의미). 그렇다면 어떻게 Rejection Sampling을 이용해서 p(z) 분포를 따르는 샘플들을 구할 수 있을까. 우선 Rejection Sampling을 사용하기 위해선 새로운 분포 q(z)를 도입해야 한다. 이 때, q(z)는 샘플을 쉽게 구할 수 있는 분포로 가정한다. proposal distribution이라고도 한다.
q(z)에 상수 k를 곱한 값을 사용하는데 kq(z)는 envelope function(포괄 함수)를 말한다. k는 kq(z)>=~p(z)를 만족하는 가장 작은 k를 사용한다.

이제 위 그림을 통해 샘플링을 수행하는 방식을 알아보자. 가장 먼저 z0을 선택해야 하는데 이 때 선택된 샘플 z0은 q(z)를 따르는 샘플이고 따지자면 p(z)와는 상관이 없다. 다음으로 균등 분포를 이용하여 [0,kq(z0)] 사이의 난수 하나를 발생시키고 이 값을 u0으로 둔다. 마지막으로 z0을 사용하여 ~p(z)를 구하는데 이 때 만약 u0<=~p(z)이면 샘플을 accept하고 아니면 reject하고 처음부터 샘플을 다시 생성하도록 한다.
Metropolis-Hastings 알고리즘
MH 알고리즘은 특정 분포를 갖는 마르코프 체인 {X0,X1,...,Xt,...}을 다음의 과정을 통해 발생시킨다. 우리가 실제로 목표로 하는 분포 p는 위에서 계속 설명했듯이 차원이 많을수록 복잡하고 구하기가 어렵다. 따라서 제안 분포 q를 샘플링하기 쉬운 가우시안 분포로 선정하고 초기 표본값을 임의로 정한 후 어떠한 규칙에 의해서 채택/기각을 시키는 것이다. 이 iteration이 계속 반복되면서 q 분포는 p 분포에 근사하게 될 것이다.
제안 분포(proposal distribution)인 q를 하나 정하는데 보통 샘플링하기 쉬운 가우시안 분포를 사용한다. 아래는 N을 각각 100, 1000, 10000로 설정했을 때, 제안분포가 얼마나 목표분포에 근사하는지를 나타낸 결과이다. N값이 커질수록 목표분포에 근접하는 것을 볼 수 있다.
N=100

N=1000
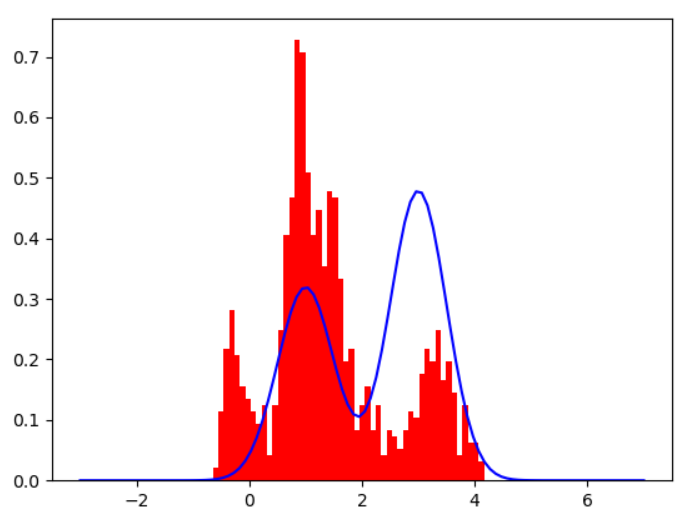
N=10000
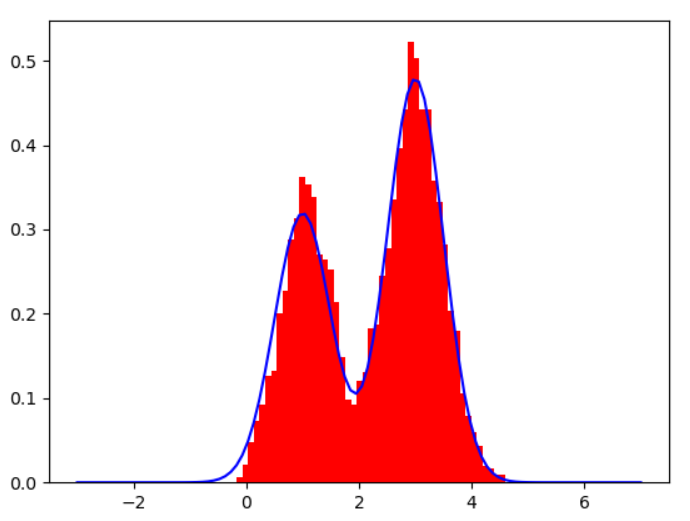
참고자료
'IT > 머신러닝' 카테고리의 다른 글
| LSH(Locality Sensitive Hashing), Minhash를 사용한 차원축소 (0) | 2020.05.14 |
|---|---|
| 아나콘다(Anaconda)에 tensorflow-cpu 설치하기 (0) | 2020.03.04 |
| 신경망의 지도학습, 델타규칙과 경사하강법 (0) | 2020.02.18 |
| 퍼셉트론의 기본 개념과 학습 규칙, 한계점 (1) | 2020.02.17 |
| sklearn을 사용한 SVM(Support Vector Machine) 분류 (7) | 2020.02.17 |