[프로그래머스] 완전탐색 - 소수 찾기 (파이썬)
- 프로그래밍/프로그래머스
- 2020. 5. 20. 00:18
프로그래머스 완전탐색 - 소수찾기, 문제 확인
숫자 조합에 관한 모든 케이스를 구한 후, 그 중 소수가 몇개인지 찾는 문제이다.
numbers는 길이 1 이상 7 이하인 문자열
numbers는 0~9까지 숫자만으로 이루어져 있음
013은 0, 1, 3 숫자가 적힌 종이 조각이 흩어져있다는 의미
흩어진 종이 조각을 붙여 소수를 몇 개 만들 수 있는지, 개수를 리턴
프로그래머스 완전탐색 - 소수찾기, 문제 풀이 (파이썬)
모든 수의 조합을 찾는 것은 itertools의 permutations를 임포트하여 구하였다. "17"의 경우 길이가 1인 경우의 조합과 2인 경우의 조합을 전부 구해야 하기 때문에 1부터 numbers 길이까지 반복문을 돌면서 모든 조합을 구해 num_case에 추가해주었다.
그리고 num_case에서 set을 사용해 중복을 제거한 후 소수 개수를 측정해주는 함수인 count_prime에 넘겨준다. count_prime에서는 2부터 n-1까지 나누면서 나누어떨어지는 것이 없는 경우 소수로 판단해 소수 리스트에 추가하고 개수를 리턴하게 하였다.
from itertools import permutations
# 인자로 받은 리스트에서 소수 개수를 측정하는 함수
def count_prime(num_case):
prime_list = []
for n in num_case:
count = 0
for i in range(2,n): # 2부터 n-1까지 나누었을 때 나머지가 0인 것은 소수가 아님
if n % i == 0: count+=1
if n > 1 and count == 0: # 나누어떨어지는게 없고 0,1이 아니면 소수 리스트에 추가
prime_list.append(n)
return len(prime_list) # 소수 리스트 개수를 리턴
def solution(numbers):
num_case = []
for i in range(1,len(numbers)+1): # 1부터 numbers 길이만큼 반복
tmp = permutations(numbers,i) # i 길이만큼의 조합을 구함
for n in tmp:
tmp_str = "".join(n) # 결과가 튜플이기 때문에 합침
num_case.append(int(tmp_str)) # int로 변형 후 리스트에 추가
num_case=list(set(num_case)) # 중복을 제거
return count_prime(num_case)
하지만, 테스트케이스 2,10에서 시간초과가 발생했다.
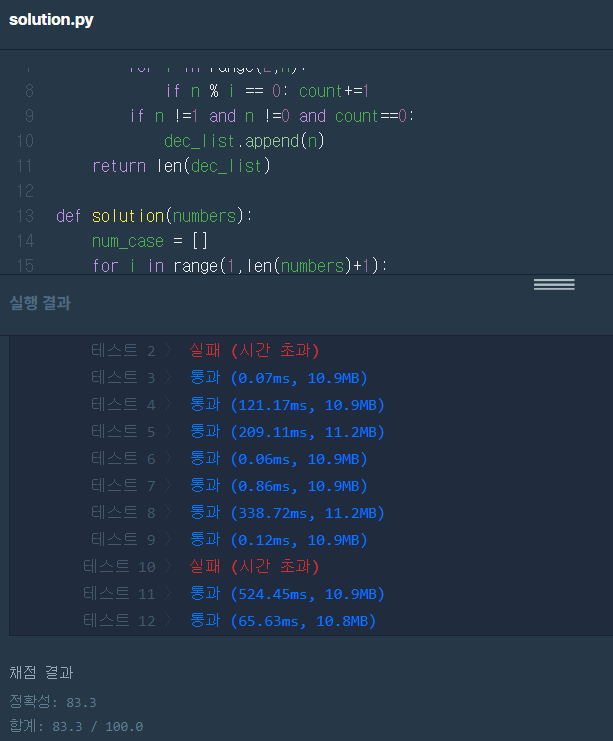
반복문 중에 시간을 줄일 수 있을만한 곳을 찾아보다가 아래 count_prime 함수에서 나누어떨어지는 경우 (=나머지가 0인 경우)에 대해 전부 count를 ++해주고 나중에 count가 0인지 확인하는 방식으로 하는게 굉장히 비효율적임을 알았다. 하나라도 나누어떨이지는 것이 있다면 소수가 아닌 것이기 때문에 그 다음 반복은 하지 않아도 되기 때문이다.
# 인자로 받은 리스트에서 소수 개수를 측정하는 함수
def count_prime(num_case):
prime_list = []
for n in num_case:
count = 0
for i in range(2,n): # 2부터 n-1까지 나누었을 때 나머지가 0인 것은 소수가 아님
if n % i == 0: count+=1
if n > 1 and count == 0: # 나누어떨어지는게 없고 0,1이 아니면 소수 리스트에 추가
prime_list.append(n)
return len(prime_list) # 소수 리스트 개수를 리턴
따라서 아래와 같이 하나라도 나누어떨어지는 것이 있으면 break 하도록 코드를 변경해주었다.
def count_prime(num_case):
prime_count = 0
for n in num_case:
count = 0
for i in range(2,n):
if n % i == 0:
count+=1
break # 하나라도 나누어떨어지는 것이 있으면 break
if n > 1 and count == 0:
prime_count += 1
return prime_count
그 결과 모든 테스트케이스를 통과할 수 있었다.

'프로그래밍 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] 탐욕법(Greedy) - 체육복 (파이썬) (0) | 2020.06.09 |
|---|---|
| [프로그래머스] 완전탐색 - 모의고사 (파이썬) (0) | 2020.05.19 |
| [프로그래머스] 정렬 - H-Index (파이썬) (0) | 2020.05.18 |
| [프로그래머스] 정렬 - 가장 큰 수 (python) (0) | 2020.05.17 |
| [프로그래머스] 정렬 - K번째수 (python) (0) | 2020.05.17 |