sklearn을 사용한 선형 회귀분석(Linear Regression)
- IT/머신러닝
- 2020. 2. 5. 18:27
파이썬 코드로 쉽게 배우는 머신러닝 시리즈 (1)
선형 회귀분석(Linear Regression)
대학원 시절, 패턴인식 과제로 수행했었던 혹은 과제 수행을 위한 선행 지식을 위해 혼자 공부했던 머신러닝, 딥러닝 관련 코드를 정리해서 올려보려 한다. 첫 시작은 선형 회귀분석이다.
참고로 본 포스팅에서는 수학적 지식은 최소한으로 다루고, 파이썬 sklearn을 사용한 선형 회귀분석의 '코드 구현과 활용'의 측면에 초점을 맞추었다.
선형회귀(Linear Regression) 모델이란?
선형회귀 모델은 지도학습 중 예측 문제에 사용하는 모델이다. 예측 문제란 기존 데이터를 기반으로 생성된 모델을 이용하여 새로운 데이터가 들어왔을 때 어떤 값이 될지 예측하는 문제를 말한다. 주식예측을 간단한 예로 들 수 있겠다(여기있는 코드는 단순선형회귀이기 때문에 실생활에 바로 응용하긴 무리가 있고 선형회귀가 무엇이고 어떻게 학습되는지 이해하는 정도로만 활용할 수 있을 것 같다). 어쨌든! 로지스틱 회귀와는 다르게 분류에 사용하지는 못하는 모델이다.
선형회귀 분석은 주어진 데이터를 표현하는 회귀선이라고 불리는 '하나의 직선'을 찾는 것에서부터 시작한다. 단순 선형회귀 분석은 x변수와 y변수 간의 관계를 y=ax+b와 같은 하나의 선형 관계식으로 표현할 수 있다. 선형 회귀분석은 최소제곱법(least square)을 기준으로 회귀선을 찾게 된다.
물론 우리는 이 모든 것을 구현하지는 않을 것이고 이미 구현된 sklearn의 LinearRegression을 가져다 쓸 것이다.
학습/테스트(Train/Test) 데이터셋 설명
학습 데이터와 테스트 데이터를 각각 plot한 아래의 결과를 보면 알 수 있다시피, 학습/테스트 데이터셋은 x,y 값으로 이루어진 아주 간단한 몇개 안되는 데이터이다.


위 데이터셋은 아래와 같이 불러올 수 있다. 학습 데이터셋은 X_tr, Y_tr 로 구성하였고, 테스트 데이터셋은 X_te, Y_te 로 구성하였다. 데이터셋 불러오는 것이야 개인 취향이기 때문에 원하는 방식으로 하면 된다.
with open('datasets/dataset2/tr_x.txt','r') as f:
self.X_tr=f.read().split('\n')
self.X_tr.pop()
self.X_tr=np.array(self.X_tr).reshape(1,-1)
self.X_tr=self.X_tr.astype(np.float).T
with open('datasets/dataset2/tr_y.txt','r') as f:
self.Y_tr=f.read().split('\n')
self.Y_tr.pop()
self.Y_tr=np.array(self.Y_tr)
self.Y_tr=self.Y_tr.astype(np.float).T
with open('datasets/dataset2/te_x.txt','r') as f:
self.X_te=f.read().split('\n')
self.X_te.pop()
self.X_te=np.array(self.X_te).reshape(1,-1)
self.X_te=self.X_te.astype(np.float).T
with open('datasets/dataset2/te_y.txt','r') as f:
self.Y_te=f.read().split('\n')
self.Y_te.pop()
self.Y_te=np.array(self.Y_te)
self.Y_te=self.Y_te.astype(np.float).T
sklearn을 사용한 선형회귀(Linear Regression) 코드
사실 sklearn을 사용하면 회귀분석에 대한 학습은 파이썬 sklearn의 LinearRegression모듈을 사용하면 단 2줄이면 끝난다. 해당 모듈을 사용하면 fit(x data, label data=y data)를 사용하여 선언해준 모델을 학습시킬 수 있다.
선형회귀 분석은 위에서도 잠깐 언급했지만, 주어진 데이터를 대표하는 하나의 직선을 찾는 것이고 이 직선을 회귀선, 그리고 이 선을 함수로 표현한 회기식을 학습으로 찾아야 한다. 즉 학습을 통해 최적의 x, y를 찾는 것이다. 단순 선형회귀 분석은 x변수와 y변수 간의 관계를 y=ax+b와 같은 하나의 선형 관계식으로 표현한다.
우리가 해줄것이라곤, 아래 코드에서 볼 수 있듯이 LinearRegression 함수를 사용해 선 객체를 선언하고 학습 데이터 x,y를 훈련 함수인 fit 에 넣어주는 것밖에 없다.
#train the model with X_tr and Y_tr
line=linear_model.LinearRegression(normalize=True)
line.fit(self.X_tr,self.Y_tr)
회귀선을 그리기 위해 x를 데이터가 존재하는 구간(0~2) 사이의 100개의 데이터로 선언해주고 y를 학습 데이터셋을 사용하여 학습한 결과로 나온 매개변수 coef와 intercept를 사용한 1차 방정식 식의 값으로 사용하였다.
즉, 학습의 결과로 coef_와 intercept_가 나오기 때문에 아래 코드에도 나와있다시피, 'coef_*X+intercept_'를 회귀 직선 식으로 사용하겠다는 뜻이다. 이제 회귀식을 구했기 때문에 회귀직선 위에 있는 데이터와 아래에 있는 데이터를 구분해서 plot시킬 수 있게된다.
#regression line in train data plot
plt.figure(3)
plt.title('Regression line in train data')
X=np.linspace(0,2,100)
plt.plot(X,line.coef_*X+line.intercept_,color='black')
for i in range(len(self.X_tr)):
if self.Y_tr[i]>=line.coef_*self.X_tr[i]+line.intercept_:
plt.scatter(self.X_tr[i],self.Y_tr[i],color='red')
if self.Y_tr[i]<line.coef_*self.X_tr[i]+line.intercept_:
plt.scatter(self.X_tr[i],self.Y_tr[i],color='blue')
선형회귀(Linear Regression) 학습 결과
아래는 각각 위에서 학습시킨 선형회귀 모델에 학습/테스트 데이터를 넣은 결과이다. 이러한 선형회귀를 예측 모델로써 활용한다는 의미는 Y값이 없는 데이터에 대해 X값으로 모르는 Y값을 예측하겠다는 뜻이 된다.

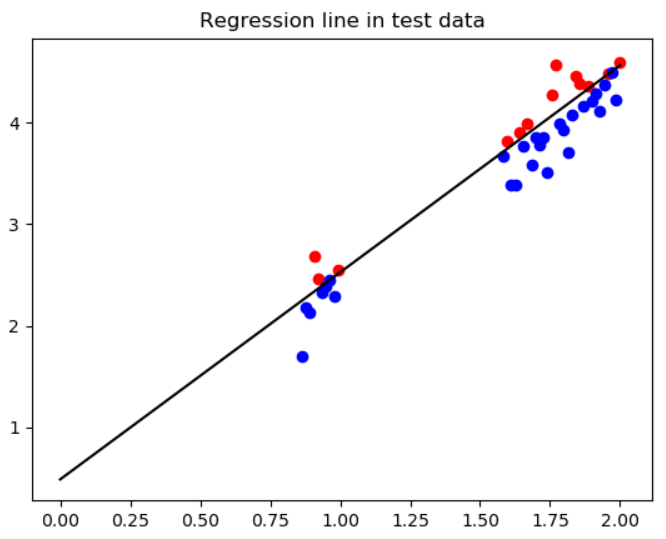
sklearn을 사용한 선형회귀(Linear Regression) 전체 코드
필요한 사람들을 위해 전체 코드를 공개한다. (필요한 사람이 없을 것 같지만 학습과 테스트 데이터는 필요하신 분은 댓글로 메일주소 달아주시면 보내드리겠습니다).
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model
from sklearn.metrics import accuracy_score
class linear:
def __init__(self):
self.X_tr=[]
self.Y_tr=[]
self.X_te=[]
self.Y_te=[]
#get datasets
def get_data(self):
with open('datasets/dataset2/tr_x.txt','r') as f:
self.X_tr=f.read().split('\n')
self.X_tr.pop()
self.X_tr=np.array(self.X_tr).reshape(1,-1)
self.X_tr=self.X_tr.astype(np.float).T
with open('datasets/dataset2/tr_y.txt','r') as f:
self.Y_tr=f.read().split('\n')
self.Y_tr.pop()
self.Y_tr=np.array(self.Y_tr)
self.Y_tr=self.Y_tr.astype(np.float).T
with open('datasets/dataset2/te_x.txt','r') as f:
self.X_te=f.read().split('\n')
self.X_te.pop()
self.X_te=np.array(self.X_te).reshape(1,-1)
self.X_te=self.X_te.astype(np.float).T
with open('datasets/dataset2/te_y.txt','r') as f:
self.Y_te=f.read().split('\n')
self.Y_te.pop()
self.Y_te=np.array(self.Y_te)
self.Y_te=self.Y_te.astype(np.float).T
#train data plot
plt.figure(1)
plt.title('Linear regression-train data')
plt.scatter(self.X_tr,self.Y_tr)
#test data plot
plt.figure(2)
plt.title('Linear regression-test data')
plt.scatter(self.X_te,self.Y_te)
def model(self,x):
return 1/(1+np.exp(-x))
def linear_regression(self):
#train the model with X_tr and Y_tr
line=linear_model.LinearRegression(normalize=True)
line.fit(self.X_tr,self.Y_tr)
#regression line in train data plot
plt.figure(3)
plt.title('Regression line in train data')
X=np.linspace(0,2,100)
plt.plot(X,line.coef_*X+line.intercept_,color='black')
for i in range(len(self.X_tr)):
if self.Y_tr[i]>=line.coef_*self.X_tr[i]+line.intercept_:
plt.scatter(self.X_tr[i],self.Y_tr[i],color='red')
if self.Y_tr[i]<line.coef_*self.X_tr[i]+line.intercept_:
plt.scatter(self.X_tr[i],self.Y_tr[i],color='blue')
#regression line in test data plot
plt.figure(4)
plt.title('Regression line in test data')
X=np.linspace(0,2,100)
plt.plot(X,line.coef_*X+line.intercept_,color='black')
for i in range(len(self.X_te)):
if self.Y_te[i]>=line.coef_*self.X_te[i]+line.intercept_:
plt.scatter(self.X_te[i],self.Y_te[i],color='red')
if self.Y_te[i]<line.coef_*self.X_te[i]+line.intercept_:
plt.scatter(self.X_te[i],self.Y_te[i],color='blue')
plt.show()
def main():
line=linear()
line.get_data()
line.linear_regression()
if __name__=="__main__":
main()
'IT > 머신러닝' 카테고리의 다른 글
| 아나콘다(Anaconda)에 tensorflow-cpu 설치하기 (0) | 2020.03.04 |
|---|---|
| 신경망의 지도학습, 델타규칙과 경사하강법 (0) | 2020.02.18 |
| 퍼셉트론의 기본 개념과 학습 규칙, 한계점 (1) | 2020.02.17 |
| sklearn을 사용한 SVM(Support Vector Machine) 분류 (7) | 2020.02.17 |
| sklearn을 사용한 로지스틱 회귀분석(Logistic Regression) (4) | 2020.02.10 |