sklearn을 사용한 로지스틱 회귀분석(Logistic Regression)
- IT/머신러닝
- 2020. 2. 10. 00:42
파이썬 코드로 쉽게 배우는 머신러닝 시리즈 (2)
로지스틱 회귀분석(Logistic Regression)
지난 포스팅에서 선형 회귀분석 (Linear Regression)에 대해 간단히 살펴보았다. 오늘은 로지스틱 회귀분석(Logistic Regression)에 대해 살펴본다. 본 포스팅은 수학적 지식은 최소한으로 다루고 파이썬 sklearn을 사용한 로지스틱 회귀분석의 '코드 구현과 활용'의 측면에 초점을 맞추었다.
로지스틱 회귀분석 (Logistic Regression) 이란?
선형 회귀와는 다르게 로지스틱 회귀는 결과가 범주형일 때 사용하기 때문에 분류 모델로 사용할 수 있다. 선형 회귀는 기본적으로 'y=ax+b'의 모습을 갖고 있었고 달라지는 x값에 대한 y값을 예측하는 것이 목표인 모델이었다. 그에 반해 로지스틱 회귀는 A,B 라는 크게 두개의 분류가 있을 때, (극단적으로 말해서) 0.5를 기준으로 그보다 큰지 작은지에 따라 A,B로 분류하자는 것이다. 즉, 로지스틱 회귀분석에서의 y는 'A'일 확률 혹은 'B일 확률'을 의미한다.
저번 선형 회귀분석 포스팅에서 선형회귀는 분류 모델로 사용하지 않는다고 했는데 왜냐하면 1차 직선식으로는 이항 분류를 하기에 적합하지 않기 때문이다. (1차 직선식으로 이항 분류를 하려면 여러가지 문제가 있다. 이에 대해선 나중에 활성함수를 다룰 때 다루려고 한다) 어쨌든 그래서 로지스틱 회귀분석에서는 1차 직선식을 시그모이드(sigmoid)라는 활성함수에 넣어서 sigmoid(y) 를 분류선으로 사용하게 된다.
그렇다면, 간단한 데이터셋과 파이썬 sklearn의 LogisticRegression 을 사용해서 데이터를 분류해보자.

학습/테스트(Train/Test) 데이터셋 설명
학습 데이터와 테스트 데이터를 각각 plot한 아래의 결과를 보면 알 수 있다시피, 학습/데이터셋은 x,y 값으로 이루어진 아주 간단한 1차원 데이터의 모습이다. 조만간 선형 회귀분석, 로지스틱 회귀분석에 좀더 직관적인? 데이터를 학습한 결과도 추가하려고 한다.


sklearn을 사용한 로지스틱 회귀분석 (Logistic Regression) 코드
파이썬 sklearn의 LogisticRegression모듈을 사용하였고 해당 모듈을 사용하면 fit(x data, label data)를 사용하여 선언해준 모델을 학습시킬 수 있다.
#train the model with X_tr and Y_tr
lr=linear_model.LogisticRegression()
lr.fit(self.X_tr,self.Y_tr)
로지스틱 회귀선을 그리기 위해 x를 데이터가 존재하는 구간(-5~5) 사이의 100개의 데이터로 선언해주고, y를 학습 dataset을 사용하여 학습한 결과로 나온 매개변수 coef_와 intercept_를 사용한 1차 방정식 식을 위에서 간단히 설명한 model 함수(시그모이드 함수)에 넣은 값으로 사용하였다.
선형 회귀분석에서 사용한 LinearRegression()과 로지스틱 회귀분석에서 사용하는 LogisticRegression() 함수 전부 fit을 사용해서 학습한 후 학습 결과로 매개변수인 coef_와 intercept_를 얻게된다. 즉, 선형 회귀분석에서는 회쉬선으로 'coef_*X+intercept_'를 사용했고 로지스틱 회귀분석에서는 sigmoid('coef_*X+intercept_')를사용하게된다.
#Sigmoid
def model(self,x):
return 1/(1+np.exp(-x))
위에서 만든 시그모이드 식에 넣은 출력값과 라벨 값을 비교하여 라벨 값이 더 크면 predict 리스트에 1 라벨을 추가하고 작으면 0 라벨을 추가하는 식으로 테스트 dataset을 분류하였다. 아래 코드가 분류된 라벨을 사용해 테스트 데이터를 색으로 분류하여 plot하는 내용이다.
즉, 아래 코드에도 나오듯 이항 분류의 식으로 sigmoid('coef_*X+intercept_')를 사용한 것이다. 또한, 분류 결과를 보기 쉽게하기 위해 색을 빨간색, 파란색으로 나누어 scatter 하였다.
#train data classification plot
predict=[]
plt.figure(3)
plt.title('Logistic regression-train data Classification')
for i in range(len(self.X_tr)):
if self.Y_tr[i]>self.model(self.X_tr[i]*lr.coef_+lr.intercept_):
plt.scatter(self.X_tr[i],self.Y_tr[i],color='blue')
predict.append(1)
if self.Y_tr[i]<self.model(self.X_tr[i]*lr.coef_+lr.intercept_):
plt.scatter(self.X_tr[i],self.Y_tr[i],color='red')
predict.append(0)
X=np.linspace(-5,5,100)
line=self.model(X*lr.coef_+lr.intercept_).ravel()
plt.plot(X,line,color='black')
sklearn을 사용한 로지스틱 회귀(Logistic Regression) 학습 결과
아래는 각각 위에서 학습시킨 로지스틱 회귀분석 모델에 학습/테스트 데이터를 넣은 결과이다. 이러한 로지스틱 회귀를 분류 모델로써 활용한다는 의미는 어떤 집단에 속하는지 모르는 데이터 X에 대해 결과 Y를 가지고 분류를 하겠다는 뜻이다.
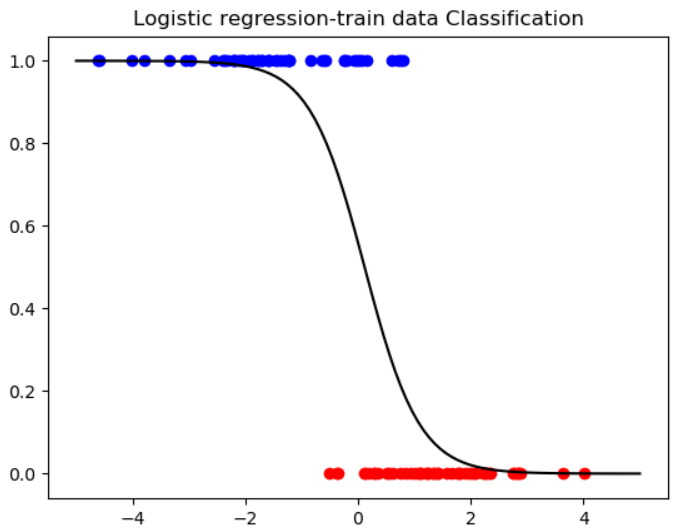

참고로, 분류 모델은 아래와 같이 정확도를 측정할 수도 있는데 이에 관한 코드는 아래 전체코드에서 확인하면 좋을 것 같다.
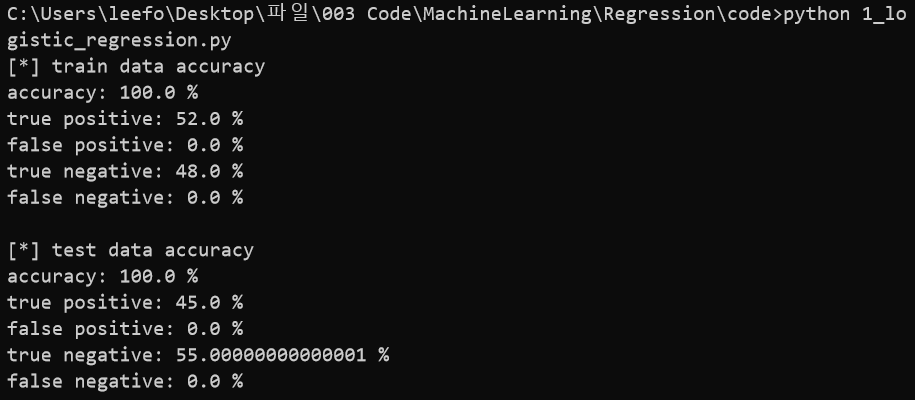
sklearn을 사용한 로지스틱 회귀분석 (Logistic Regression) 전체 코드
로지스틱 회귀분석을 통한 데이터셋 분류 전체 코드는 아래와 같다.
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model
class logistic:
def __init__(self):
self.X_tr=[]
self.Y_tr=[]
self.X_te=[]
self.Y_te=[]
def get_data(self):
with open('datasets/dataset1/tr_x.txt','r') as f:
self.X_tr=f.read().split('\n')
self.X_tr.pop()
self.X_tr=np.array(self.X_tr).reshape(1,-1)
self.X_tr=self.X_tr.astype(np.float).T
with open('datasets/dataset1/tr_t.txt','r') as f:
self.Y_tr=f.read().split('\n')
self.Y_tr.pop()
self.Y_tr=np.array(self.Y_tr)
self.Y_tr=self.Y_tr.astype(np.float).T
with open('datasets/dataset1/te_x.txt','r') as f:
self.X_te=f.read().split('\n')
self.X_te.pop()
self.X_te=np.array(self.X_te).reshape(1,-1)
self.X_te=self.X_te.astype(np.float).T
with open('datasets/dataset1/te_t.txt','r') as f:
self.Y_te=f.read().split('\n')
self.Y_te.pop()
self.Y_te=np.array(self.Y_te)
self.Y_te=self.Y_te.astype(np.float).T
#train data plot
plt.figure(1)
plt.title('Logistic regression-train data')
for i in range(len(self.X_tr)):
if self.Y_tr[i]==0:
plt.scatter(self.X_tr[i],0,color='blue')
for i in range(len(self.X_tr)):
if self.Y_tr[i]==1:
plt.scatter(self.X_tr[i],0,color='red')
#test data plot
plt.figure(2)
plt.title('Logistic regression-test data')
for i in range(len(self.X_te)):
if self.Y_te[i]==0:
plt.scatter(self.X_te[i],0,color='blue')
for i in range(len(self.X_te)):
if self.Y_te[i]==1:
plt.scatter(self.X_te[i],0,color='red')
#Sigmoid
def model(self,x):
return 1/(1+np.exp(-x))
def logistic_regression(self):
#train the model with X_tr and Y_tr
lr=linear_model.LogisticRegression()
lr.fit(self.X_tr,self.Y_tr)
#train data classification plot
predict=[]
plt.figure(3)
plt.title('Logistic regression-train data Classification')
for i in range(len(self.X_tr)):
if self.Y_tr[i]>self.model(self.X_tr[i]*lr.coef_+lr.intercept_):
plt.scatter(self.X_tr[i],self.Y_tr[i],color='blue')
predict.append(1)
if self.Y_tr[i]<self.model(self.X_tr[i]*lr.coef_+lr.intercept_):
plt.scatter(self.X_tr[i],self.Y_tr[i],color='red')
predict.append(0)
X=np.linspace(-5,5,100)
line=self.model(X*lr.coef_+lr.intercept_).ravel()
plt.plot(X,line,color='black')
#accuracy,true positive,false positive,false negative,true negative of train data
tp=0; fp=0; tn=0; fn=0
for i in range(len(predict)):
if predict[i]==self.Y_tr[i]:
if predict[i]==1:
tp+=1
if predict[i]==0:
tn+=1
if predict[i]!=self.Y_tr[i]:
if predict[i]==1:
fn+=1
if predict[i]==0:
fp+=1
print('[*] train data accuracy')
print('accuracy:',(float(tp+tn)/len(predict))*100,'%')
print('true positive:',(float(tp)/len(predict))*100,'%')
print('false positive:',(float(fp)/len(predict))*100,'%')
print('true negative:',(float(tn)/len(predict))*100,'%')
print('false negative:',(float(fn)/len(predict))*100,'%')
#test data classification plot
predict=[]
plt.figure(4)
plt.title('Logistic regression-test data Classification')
for i in range(len(self.X_te)):
if self.Y_te[i]>self.model(self.X_te[i]*lr.coef_+lr.intercept_):
plt.scatter(self.X_te[i],self.Y_te[i],color='blue')
predict.append(1)
if self.Y_te[i]<self.model(self.X_te[i]*lr.coef_+lr.intercept_):
plt.scatter(self.X_te[i],self.Y_te[i],color='red')
predict.append(0)
X=np.linspace(-5,5,100)
line=self.model(X*lr.coef_+lr.intercept_).ravel()
plt.plot(X,line,color='black')
plt.show()
#accuracy,true positive,false positive,false negative,true negative of test data
tp=0; fp=0; tn=0; fn=0
for i in range(len(predict)):
if predict[i]==self.Y_te[i]:
if predict[i]==1:
tp+=1
if predict[i]==0:
tn+=1
if predict[i]!=self.Y_te[i]:
if predict[i]==1:
fn+=1
if predict[i]==0:
fp+=1
print('\n[*] test data accuracy')
print('accuracy:',(float(tp+tn)/len(predict))*100,'%')
print('true positive:',(float(tp)/len(predict))*100,'%')
print('false positive:',(float(fp)/len(predict))*100,'%')
print('true negative:',(float(tn)/len(predict))*100,'%')
print('false negative:',(float(fn)/len(predict))*100,'%')
def main():
l=logistic()
l.get_data()
l.logistic_regression()
if __name__=="__main__":
main()
데이터셋 첨부파일
'IT > 머신러닝' 카테고리의 다른 글
| 아나콘다(Anaconda)에 tensorflow-cpu 설치하기 (0) | 2020.03.04 |
|---|---|
| 신경망의 지도학습, 델타규칙과 경사하강법 (0) | 2020.02.18 |
| 퍼셉트론의 기본 개념과 학습 규칙, 한계점 (1) | 2020.02.17 |
| sklearn을 사용한 SVM(Support Vector Machine) 분류 (7) | 2020.02.17 |
| sklearn을 사용한 선형 회귀분석(Linear Regression) (5) | 2020.02.05 |